La vita di uno dei più grandi matematici, logici, criptanalisti, biologici teorici e, ovviamente, informatici iniziò il 23 giugno 1912 a Paddington, Londra. Alan Turing era tutto questo e ciò lo rende una figura estremamente interessante perché in qualunque campo (o quasi) in cui si cimentò, non sono mancate sue scoperte, estremamente rivoluzionarie.
Molto spesso, quando era ancora un ragazzino, la sua casa diventava un piccolo laboratorio dove fare esperimenti. La sua distrazione e il suo disordine si sono subito manifestati creandogli problemi con i professori e con tutto quello riguardava la disciplina.
Nonostante il suo approccio pratico alle cose, al college scelse di studiare una branca della matematica detta matematica pura. Fu proprio in questo periodo della sua vita che produsse il primo importante risultato: “On Computable Numbers”.
Indice dell'articolo
La logica e l’Entscheidungsproblem
Alla fine dell’Ottocento si insinuò nella mente di certi matematici l’idea che Euclide fosse stato frettoloso nella scrittura di uno dei cinque postulati.
“Date due rette parallele tagliate da una trasversale, la somma dei due angoli coniugati interni è pari ad un angolo piatto”.
Provando a dimostrare questa “verità”, o meglio, assioma, scoprirono che essa poteva tutt’altro che definirsi tale. Il problema stava nel fatto che Euclide si era basato su idee intuitive: era arrivato il momento di astrarre i concetti di linee e punti e dimostrare che il postulato restava immutato. Non a caso, era in quel periodo che si sviluppava la logica e la matematica si portava a basarsi più sui simboli che non sui numeri.
Uno dei primi matematici ad occuparsi di ciò fu David Hilbert, seguito da Bertrand Russell, Alfred North Whitehead, Gottlob Frege e tanti altri. L’essenza della questione divenne quello di cercare le idee logiche più primitive da cui si potesse dedurre la matematica. L’approccio usato da Hilbert fu quello formalista. Egli si propose di rispondere a tre domande per poter salvare la matematica.
- La matematica è completa? Se ogni enunciato fosse dimostrabile o refutabile.
- La matematica è coerente? Se ci siano enunciati che si contraddicono tra loro.
- La matetica è decidibile? Se esista un metodo applicabile ad ogni asserto che ne dimostrasse la sua veridicità.
On computable numbers
Le domande non trovarono risposta, finché non arrivò Kurt Gödel. Egli riuscì a dimostrare che la matematica non poteva essere allo stesso tempo sia coerente che completa e che certamente essa era incompleta. Tuttavia, anche lui non fu in grado di rispondere al terzo quesito. Non riuscì a risolvere l’Entscheidungsproblem ovvero il problema di decidere la dimostrabilità di qualsiasi proposizione matematica.
Max Newman cominciò a pensare che potesse esistere un processo meccanico seguendo il quale ogni proposizione matematica potesse essere decisa. Alan Turing dovette aver seguito le sue lezioni a Cambrige perché fu proprio allora che ebbe l’idea di scrivere il suo primo importante e pubblicabile testo “On computable numbers”.
La macchina di Turing
La macchina dal nastro infinito, non si preoccupava (almeno per il momento) dei problemi tecnici che sarebbero nati nella realizzazione. Essa fu concepita solo per quello che teoricamente e logicamente essa avrebbe potuto fare.
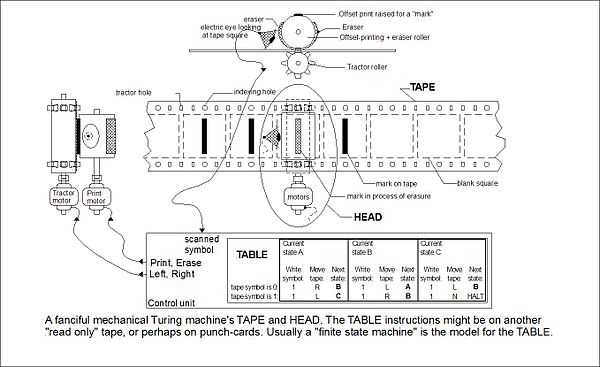
La macchina doveva possedere un numero finito di configurazioni interne, una posizione variabile sulla riga di scrittura. Inoltre l’azione della macchina non doveva dipendere da quella posizione. Alan Turing la immaginò come un nastro infinito. Su di esso ci dovevano essere delle caselle in ciascuna delle quali si poteva scrivere un simbolo.
La funzione della macchina era quella di leggere, aggiungere un simbolo se la casella era vuota, lasciare immutato quello presente o cancellarlo. In seguito doveva cambiare configurazione proseguendo a destra o sinistra, di un posto alla volta o restava nella casella in cui si trovava. Essa era quindi programmata per compiere atti di riconoscimento e di decisione.
L’argomento diagonale di Cantor
Ma torniamo al problema di Hilbert. Al fine di risolvere la questione scatenata dalla rivoluzione scientifica di fine ottocento egli usò dei numeri detti computabili. I numeri computabili sono quelli che possono essere calcolati per mezzo di un processo meccanico (una serie di regole ben definite). Un esempio di un processo che, teoricamente, poteva essere fatto dalla macchina era l’argomento diagonale di Cantor.
| 1 | 0,500000000000000000 |
| 2 | 0,333333333333333000 |
| 3 | 0,250000000000000000 |
| 4 | 0,666666666666666000 |
| 5 | 0,200000000000000000 |
| 6 | 0,166666666666666000 |
| 7 | 0,400000000000000000 |
| 8 | 0,750000000000000000 |
Nella tabella in alto sono mostrati i numeri decimali dati da 1/2, 1/3, 1/4 e così via in modo da scrivere tutti i numeri razionali esistenti. Ora, prendendo i numeri sulla diagonale (numeri in grassetto) e sommando a ciascuno un’unità si ottiene il numero 0, 64171711…
Questo numero di sicuro non può essere tra quelli della tabella (avendo almeno una cifra incrementata di uno) ma, pertanto, non può nemmeno essere un numero razionale. Questo metodo restava ben definito seppure generasse un numero irrazionale a partire da irrazionale. E, soprattutto, richiedeva un tempo infinito per essere calcolato.
Applicazione al problema dell’ Entscheidungsproblem
Ma qui sta la risposta al problema della decisione. Mettiamo il caso di trovarci a dimostrare una proposizione matematica (trasformandola con simboli logici, come aveva già precedentemente fatto Gödel). La dimostrazione di questa consiste in un metodo chiaramente definito ma che richieda un tempo infinito. Ovvero non potrò dimostrare che, ad un certo passaggio, ad una certa tavola di istruzioni, la macchina potrebbe incepparsi e non terminare il suo lavoro. Non c’è modo di controllare in anticipo se la tavola di istruzioni fosse in grado di produrre una sequenza infinita. Non si può aspettare un tempo infinito per vedere se la soluzione è giusta: abbiamo trovato un problema insolubile.
Questo articolo ebbe moltissimo successo e fu citato da molti di quelli che avrebbero preso parte all’invenzione del computer.
AlanTuring non aveva solo risolto un problema aveva inventato l’idea della macchina universale.
Mina Nardo

